はじめに
こんにちは、ゆとり世代の福治です。 ゆとり世代は高校までの数学だと、データの概要を把握するときの値って、平均値と最小値、最大値ぐらいしか習ってない気がするんですよね。
今回は、データの簡単な特徴を把握する際に、平均値だけをみてしまいがちになってしまっているのではないのかという問題提起とともに、平均値だけでデータを把握してしまわないようにするにはどうすれば良いのかをお話ししようと思います。
サンプルデータ
今回、以下の3つの例をあげて説明していきたいと思います。いずれも平均10.5のデータになります。
| データ | 平均 | |
|---|---|---|
| 例1) | 1、2、3、4、5、6、7、8、9、10、11、12、13、14、15、16、17、18、19、20 | 10.5 |
| 例2) | 10、10、10、10、10、10、10、10、10、10、11、11、11、11、11、11、11、11、11、11、 | 10.5 |
| 例3) | 1、1、1、1、1、1、1、1、1、1、20、20、20、20、20、20、20、20、20、20 | 10.5 |
平均値だけで判断してしまう危険性
サンプルデータはどれも平均値が同じため、平均値だけでデータの特徴を捉えてしまうと、どれも同じようなデータということになってしまいます。
仮に、サンプルデータが毎月20枠付与されるサービスの使用状況だとしましょう。 (1だったら1枠使用、2だったら2枠使用…) また、例1)はある月、例2)は翌月、例3)はさらに翌月だということにします。 すると、どうでしょうか?平均値だけでみてしまうと、毎月使用状況は変わらないように見えますが、データの中身をきちんとみると、かなり状況が違うことがわかると思います。
今回、サンプル数が少ないため一見しただけで極端なデータであることがわかる人もいるかもしれません。しかし、大きなデータを扱う際は全ての数字をみることは不可能なので、偏ったデータであることに気がつかず、平均値だけで判断し、間違った認識を持ってしまう危険性はかなり高いです。
平均値だけで判断してしまわないように
平均値だけで判断してしまわないようにいくつかの方法があります。その中で今回は、一部にはなりますが2つをお伝えしたいと思います。
- 箱ひげ図を書いてみる。
- ヒストグラムを書いてみる。
1. 箱ひげ図を書いてみる。
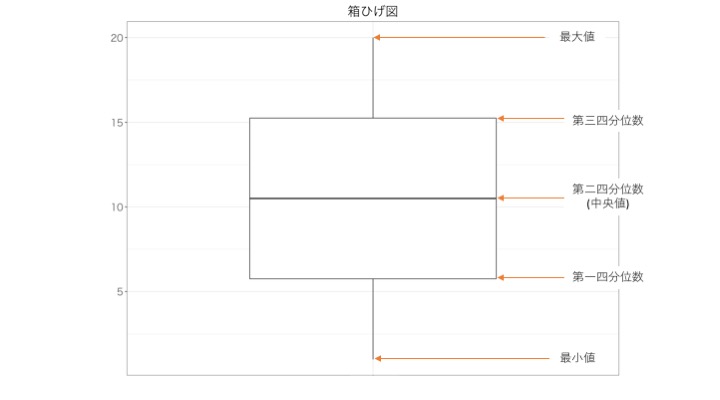
箱ひげ図と聞いて、何だろうそれはと思う人もいると思います。 箱ひげ図を書くには、四分位数というものを求める必要があります。 順を追って説明していきますので、まず四分位数について説明します。
四分位数とは統計WEBによると、以下の定義になります。
データを小さい方から並び替え、データの個数(サンプルサイズ)で4等分した時の区切り点を四分位数と言う。それぞれ25パーセンタイル(第一四分位数)、50パーセンタイル(中央値)、75パーセンタイル(第三四分位数)とよばれる。
サンプルデータに当てはめてみると、いずれもサンプル数が20なので、第一四分位数は5番目と6番目の平均値、第二四分位数(中央値)は10番目と11番目の平均値、第三四分位数は15番目と16番目の平均値となります。
| 第一四分位数 | 第二四分位数(中央値) | 第三四分位数 | |
|---|---|---|---|
| 例1) | 5.5 | 10.5 | 15.5 |
| 例2) | 10 | 10.5 | 11 |
| 例3) | 1 | 10.5 | 20 |
※少し余談 今回サンプルデータなので、第二四分位数(中央値)と平均値が一緒になっていますが、この二つの違いがわかってないと、「ウチの子は平均点より高いのにクラス内順位が真ん中より低いなんておかしい!(参照)」なんてことになっちゃったりします。
さて、四分位数に関して理解することができたら、箱ひげ図についての説明をしたいと思います。 箱ひげ図を書くには、四分位数に加え、最大値、最小値が必要になります。
上の表に最大値と最小値を加えたものが以下の表になります。
| 最小値 | 第一四分位数 | 第二四分位数(中央値) | 第三四分位数 | 最大値 | |
|---|---|---|---|---|---|
| 例1) | 1 | 5.5 | 10.5 | 15.5 | 20 |
| 例2) | 10 | 10 | 10.5 | 11 | 11 |
| 例3) | 1 | 1 | 10.5 | 20 | 20 |
さあ、箱ひげ図を書く準備ができました。箱ひげ図は以下のように書きます。 ※下の図で最大値と最小値と書かれている部分に関しては、原則最大値と最小値が書かれるのですが、異なる場合もあります。
実際にこのように例のデータを当てはめると、以下のようになります。
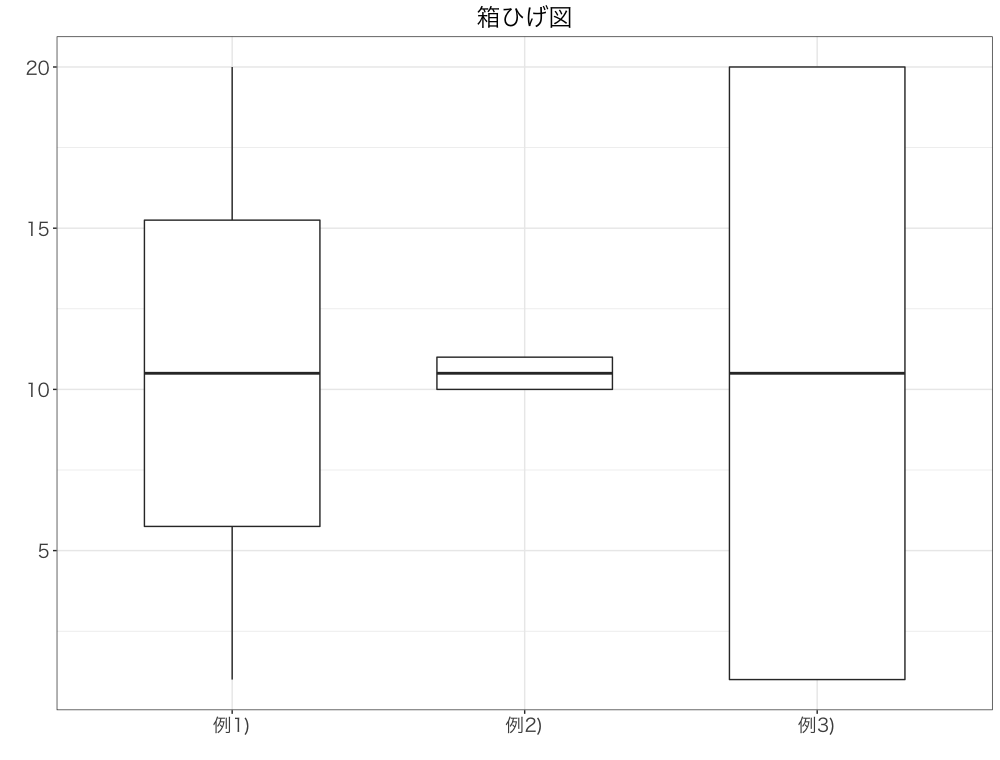
こうやってみると、同じ平均値のデータでも、全然特徴が違うことがすぐにわかると思います。 ただ、勘のいい人だとお気づきかもしれませんが、四分位数も2つの値の平均になってしまっている部分に関しては、その値でいいの?!ってなっているかもしれません(特に例3)の第二四分位数)。そこで、次にこの問題点を解決するものとして、ヒストグラムというものをご紹介します。
2. ヒストグラムを書いてみる。
IT用語辞典によると以下のように定義されています。
ヒストグラムとは、データの分布を表す統計図の一つで、縦軸に値の数(度数)、横軸に値の範囲(階級)を取り、各階級に含まれる度数を棒グラフにして並べたもの。値の出現頻度の高い階級は高い棒で、低い階級は低い棒で図示されるため、出現頻度の高低やバラつき具合を視覚的に容易に把握できる。
つまりは、値の範囲(階級)とその範囲内にあるデータの数(度数)をグラフにしたものです。
例えば、以下のデータがあるとします。
1、3、4、4、6、7、10
例えば、値の範囲を3つづつ取る(階級幅を3)とすると、以下の表ができ、さらにそれをヒストグラムに表すと以下のようになります。 ※原則として、階級はAからBまでだった場合、A<データ≦Bとなり、最小値と最大値に関してはそれぞれ最初の区間、最後の区間に含まれます。 ※階級幅は、適切な範囲を計算によって求められる手法がいくつかありますが、その都度どのくらいの粒度で確認したいかによっていくつか書いてみて適切に変えてもらえれば十分かなと思います。
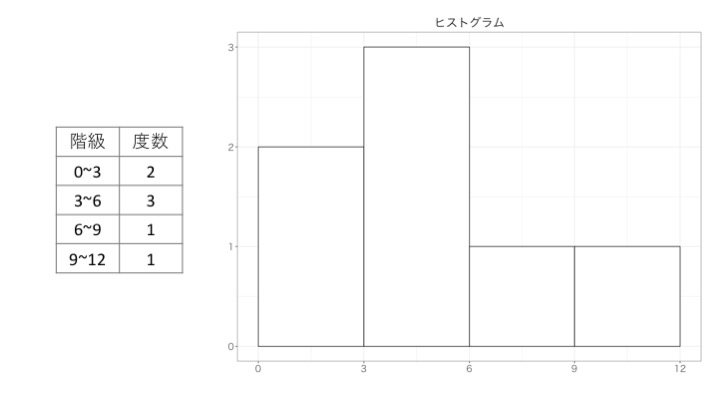
では実際に3つの例で書いてみましょう。(階級幅は2にしています。)
例1)では、0~2が2つ、2~4が2つ、4~6が2つ…と全ての度数が2つづつなので、以下のようなヒストグラムになります。
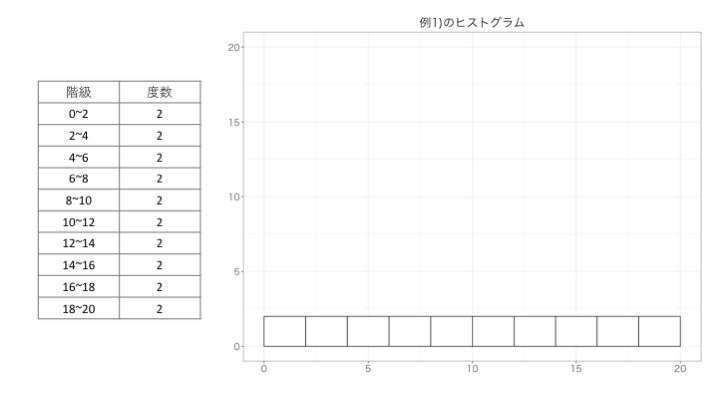
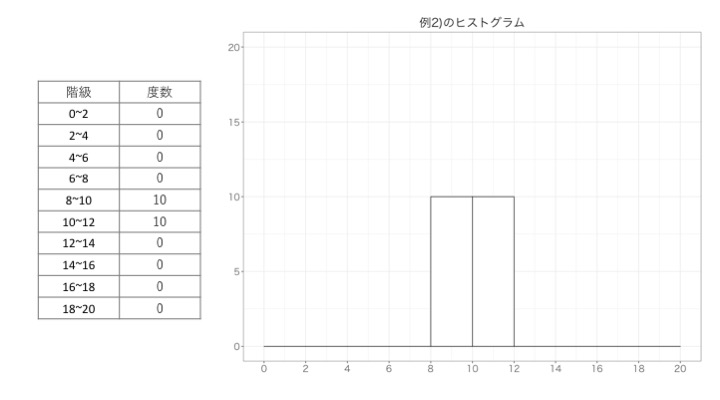
例2)では、8~10、10~12がそれぞれ10個づつあるので、以下のようなヒストグラムになります。
例3)では、0~2と19~20がそれぞれ10個づつあるので、以下のようなヒストグラムになります。
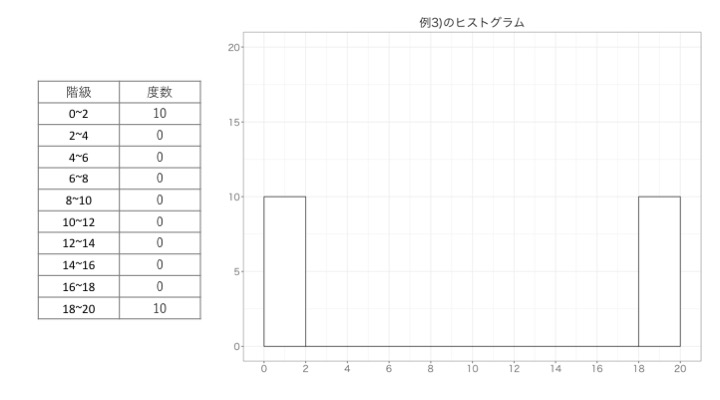
このようにヒストグラムを書くことによって、どの数字にどのくらいの偏りがあるのかをぱっと見で判断できるようになります。
終わりに
今回は、平均値だけでデータを判断しないためにどうすれば良いのかを書いてみました。 みなさんが何を使ってデータの概要を把握するのかがわからなかったので、特にグラフの書き方は載せていません。(もし、興味のある人は、ググってみてください。)
また、今回は紹介しませんでしたが、他の方法としましては分散や標準偏差を出してみたり、データによっては外れ値を除いて分析をしてみたりする方法があげられます。
平均値が出ていて、それっぽいからと言ってそれだけでは何の情報にもなっていないこともあるので、データを細かくみれているのかを気にするようにしてみてください。
福治菜摘美
新米エンジニアです。



