2023-12-19Advent Calendar 2023, JPEG, 圧縮処理, 画像処理

この記事はレコチョク Advent Calendar 2023の19日目の記事となります。

この記事について

弊社レコチョクでバックエンドエンジニアをしています小河です。

この記事では、破損したJPEG画像をバイナリベースで解析し、なぜ破損しているのかを探ります。
その中でJPEG画像がどのように構成されているか、どのように作られているかも触れていくので、
JPEGを理解する助けにもなれるかと思います。

前提知識として以下のものが必要になるのでご留意ください。

必須な知識

• n進数の概念
• ビット・バイトの概念

あった方が良い知識

• JPEGにおける直流成分(DC成分)・交流成分(AC成分)・DCT(離散コサイン変換)・量子化・DQTセグメントの概念について
  • 以前書いたJPEG画像の「品質」は何が司っているのか – レコチョクのエンジニアブログを読んでもらえるとインプットできます
• ハフマン符号

目次

• 前段
• 問題の画像ファイルを観察する
  • メタ情報を見る
  • 見た目上の特徴
  • 画像ビューワー間での見え方の違い
  • 総括
• 大雑把にバイナリベースで画像を観察する
• JPEG形式に圧縮されるまでの流れ
  • ①YCbCr形式への変換
  • ②8ピクセル x 8ピクセルのブロックに分ける
  • ③DCT(離散コサイン変換)
  • ④量子化
  • ⑤エントロピー符号化
• 試しにイメージデータを見てみる
• DHTセグメントについて
  • 概要
  • DHTセグメントは何を表現しているのか
  • DC成分に紐づくDHTセグメント
  • AC成分に紐づくDHTセグメント
  • DHTセグメントの解析結果
• イメージデータを読み解く
  • 問題の画像のイメージデータについて
  • 改ざん前のイメージデータについて
• なぜ画像がおかしくなっていたのか？
  • 左上の市松模様のようなノイズが何個か続いているのはなぜか？
  • 元画像と比べて全体的な色味が赤くなっているのはなぜか？
• 最後に

前段

レコチョクでは展開している各サービス内で、画像を表示する必要があります。
アルバムのジャケット写真が良い例かと思います。
ちなみに弊社が展開している「レコチョク」だとこんな感じでジャケット写真を表示します↓

(このアルバムだと「未来未来」が一番好きです)

そのような画像を表示するために、フロントエンド(各サービス)からのリクエストに応じて、
特定の画像を返すシステムをバックエンド側に持っています。
パラメータに応じて、リサイズ処理も行います。

このシステムは弊社の中では「画像サーバー」と呼ばれているため、以降もその名前で扱います。

私はこの画像サーバーの保守運用を行なっているのですが、あるサービス担当者からこのような問い合わせがきました。
「画像サーバーから取得したあるジャケット写真の見た目がおかしい」

実際のジャケット写真はお見せできないので、同事象を意図的に引き起こした画像をご覧ください。

本来はこうあるべきでした。

原因を調査した結果、画像サーバー内のリサイズ処理に使っているモジュールに異常があると特定できました。
そのモジュールのバージョンを上げるとこの事象は発生しなくなったためです。

ただ、この画像ファイルには一体何が起こっていたのかが気になりました。
後学のために、問題の画像ファイルについて詳しく調べてみることにしました。

問題の画像ファイルを観察する

ひとまず、問題の画像ファイルについてざっと特徴を見ていきます。

メタ情報を見る

そもそもですが、この画像ファイルはJPEG形式のものです。
したがって、 fileコマンドでJPEGとして認識されるか見てみると、、、認識されているようです。

このファイルのメタ情報を見てみたいので、ExifToolの結果を見てみます。
特に際立ったものはありません。

見た目上の特徴

改めて問題の画像を見てみると、このような特徴があります。
1. 左上の市松模様のようなノイズが何個か続いている
1. 元画像と比べて、全体的な色味が赤っぽくなっている

画像ビューワー間での見え方の違い

この画像ですが、実は画像ビューワーによって表示のされ方が違います。
Google ChromeやGIMPではこのように表示されますが…

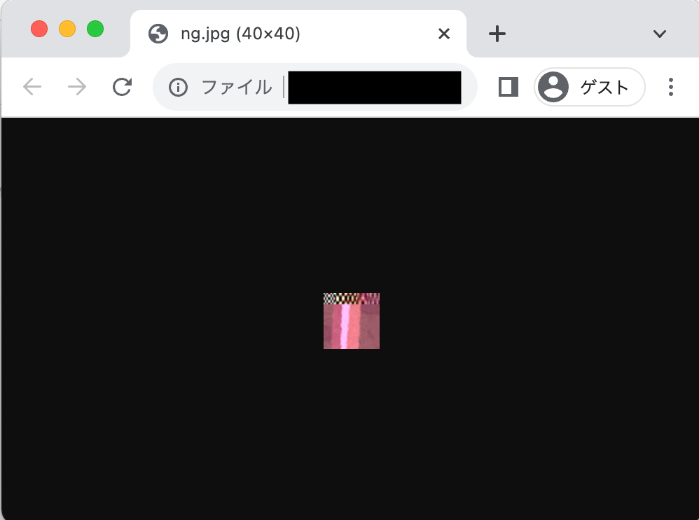
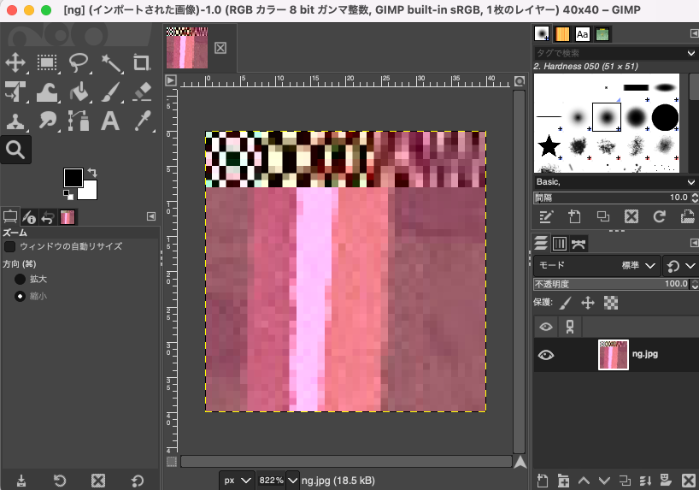
macosのプレビューだとこのように、最初は表示されていますが、途中からは灰色で埋められています。

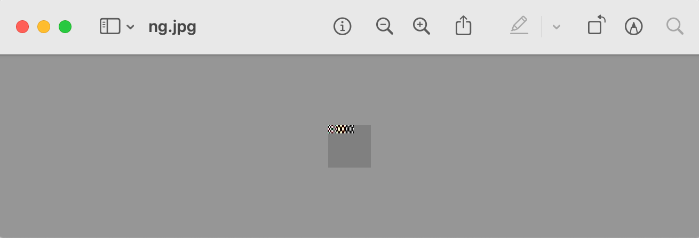
上記の結果から、以下のような仮説が立てられます。

• 問題の画像にはJPEG形式として見た時に、一部不正な箇所がある
• ビューワーやビューワーが利用しているJPEGのデコーダーによって画像を読み込むための方法が異なる
  • 前者の全て表示されるビューワーの場合、不正な箇所があっても無理やり読んでしまう仕様になっている
  • 後者のビューワーの場合、不正な箇所があった場合、その時点で表示をやめてしまう

総括

• メタ情報(Exif)には問題はない可能性が高い
• JPEG画像として見た時に、不正な箇所がある可能性が高い

したがって、メタ情報以外の部分について問題がありそうです。
少し大変ですが、バイナリベースで問題の画像を観察してみることにします。

大雑把にバイナリベースで画像を観察する

ただただ16進ダンプを見ても辛いので、fqで問題の画像を見てみます。

結果を以下に記載します。
右端の列にどのような情報が含まれているかが表示されます。

結論、ここに表示されているものについては違和感がありません。
JPEGはいくつかのセグメントという部分に分かれているのですが、必ず入っていなければならないセグメントが含まれているからです。

これは先ほどの fqの実行結果のうち、右端の列の先頭を切り出したものです。

ここに見えている範囲では SOIや APP0というセグメントが含まれています。

ここは SOIセグメントが存在していることを示しています。
ちなみにこのセグメントは、JPEGファイルの始まりを示す役割があります。

ここは APP0セグメントが存在していて、かつそこにどういった情報が入っているかを示しています。
ちなみにこのセグメントは、JFIFという規格で設定されたメタ情報を含みます。

先ほど取り上げたセグメントも含めて、下記のようなセグメントが画像に含まれていました。
必須とされるセグメントは全て含まれていました。
※ 各セグメントごとに説明は書いていますが、よく分からなければ読み飛ばしてもらって構いません

• SOI(Start Of Image)
  • 固定で 0xFF 0xD8が設定されていて、JPEGファイルの始まりを指します。
• APP0(Application0)
  • JFIFと呼ばれるメタ情報です。JFIFはExifの前身ですが、この 画像のようにExif(APP1)と同居している時もままあります。
• APP1(Application1)
  • 実はExifの情報はこのセグメントに含まれています。
• DQT(Define Quantization Table)
  • JPEGは圧縮の際に量子化(Quantization)という過程を挟みます。その時にどの程度の量子化を行うかを定義しています。
  • 以前に書いた記事内で、大雑把にですが解説しています(JPEG画像の「品質」は何が司っているのか – レコチョクのエンジニアブログ)。
• SOF(Start Of Frame)
  • JPEGファイルの種類や画像サイズといった基本的な情報が含まれています。
  • DQTをどのように適用するかという情報も入っています。
• DHT(Define Huffman Table)
  • DQTによって量子化されたデータは最終的にハフマン符号に変換されます。どのような法則で符号化されるのかが示されています。
• SOS(Start Of Scan)
  • この後にイメージデータ(ハフマン符号化された画像そのものを表すデータ)が続くことを示します。
  • イメージデータについての設定情報も含まれます。
• EOF(End Of Image)
  • 固定で 0xFF 0xD9が設定されていて、JPEGファイルの終わりを指します。

先述したように、必要なセグメントは含まれているようなので、JPEGの構造がおかしいという可能性は低めだとわかってきました。
そうすると、イメージデータ(符号化された画像そのものを表すデータ)が怪しい気がしてきます。
問題の画像ファイルのイメージデータを自力でデコードして調べてみることにします。

ただ、デコードするためにいくらかJPEGについての知識をインプットする必要がありますので、しばらくお付き合いください…。

JPEG形式に圧縮されるまでの流れ

例外もありますが、大体は以下のフローで圧縮が行われます。

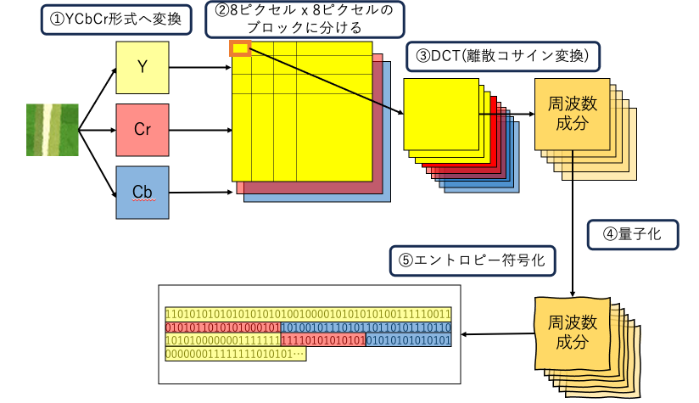
①YCbCr形式への変換

色を表現する方式としてRGB方式があまりに有名ですが、JPEGの場合は内部的にYCbCr形式を使います。
RGBはR→赤、G→緑、B→青の3つの要素で特定の色を表現します。
その一方でYCbCrはY→輝度、Cb→青み、Cr→赤みで色を表現します。
ちなみに、CbとCrは一般に色差と総称されます。

なぜYCbCr方式が良いのかというと、圧縮に有利だからです。
「人間の視覚は輝度(Y)の変化には敏感だが、色(Cb・Cr)の変化には比較的鈍感だ」という性質があります。
したがって、輝度(Y)の成分より、色(Cb・Cr)の成分をより強く圧縮することが可能になります。

以降の処理はY・Cb・Crという3つの成分に対して、それぞれ別々に処理が行われます。

②8ピクセル x 8ピクセルのブロックに分ける

Y・Cb・Crという3つの成分に対して、それぞれ8ピクセル x 8ピクセルのブロックに分けます。
以降の処理はこの8×8のブロックごとに、それぞれ別々に処理が行われます。

③DCT(離散コサイン変換)

8×8のブロックごとにDCT(離散コサイン変換)を行います。
DCTを行うことで、画像を周波数成分へ変換することができます。
周波数成分？？と思われる方は、こちらの記事で説明していますので参照ください
→ JPEG画像の「品質」は何が司っているのか – レコチョクのエンジニアブログ

ひとまずこの記事では、以下のことが把握できていれば問題ありません:

• DCTを行うと、周波数成分へ変換される
• 周波数成分には、全体的な色味を司るDC成分と、主に色の変化を司るAC成分に分けられる
• 一つの8×8のブロックごとに1つのDC成分と63個のAC成分が生み出される

④量子化

DCTによって生成された周波数成分に対して、量子化を行います。
量子化についてもこちらの記事で解説しています
→ JPEG画像の「品質」は何が司っているのか – レコチョクのエンジニアブログ

ひとまずこの記事では、以下のことが把握できていれば問題ありません:

• 量子化によって、周波数成分を示すデータの精度が落とされる(圧縮される)

⑤エントロピー符号化

量子化されたデータを符号化します。
符号化にはほとんどの場合、ハフマン符号が使われます。(算術符号が使われることも稀にあるようです)

こうしてできた符号は SOSセグメントの後にイメージデータとして配置されます。
イメージデータのイメージ図を以下のように示します。
図で示したように、1つ目のブロックのY(輝度)、1つ目のブロックのCr(色差)、1つ目のブロックのCb(色差)、2つ目のブロックのY(輝度)…という順番にデータが配置されます。

上の図ではデータの内容を適当に 1101010101という感じで表現していましたが、この正体は周波数成分です。
(③で周波数成分へ変換されているので)
周波数成分は1つのDC成分と63個のAC成分に分けられる訳ですが、それらはこのように配置されています。
DC成分が先頭に配置され、そこからAC成分がずらずらと並んでいきます。

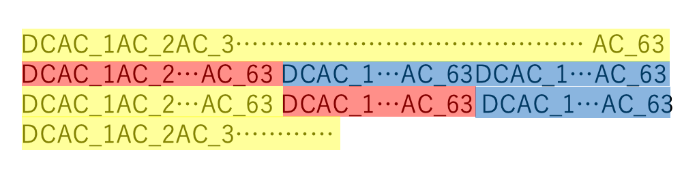
また、それぞれのDC成分やAC成分は-127 ~ 127の数値で表されます。
DC成分についてだけは、前のブロックの数値からの差分を表現しています。
1つ目のブロックのDC成分だけは実際の数値を表現します。
2つ目以降のブロックについては、ひとつ前のブロックのDC成分からの差分値を表現します。

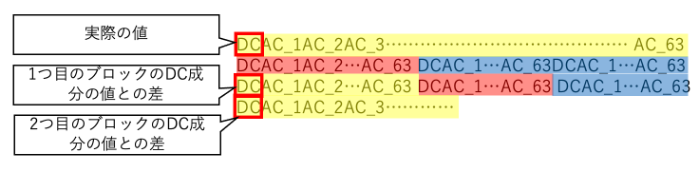
例:

何個目のブロックか	前のブロックの値との差分	値
1	–	100
2	0	100
3	1	101
4	2	103
5	0	103

の場合、100→0→1→2→0という値が記録されます。

この差分値だけで表現する方法を差分符号化と呼びます。
差分符号化は、表現したいデータの値が似通っている時にはデータ量を少なくできる(圧縮できる)という利点があります。
一方で、データの改ざんにはめっぽう弱いという弱点があります。

例えば、3つめのブロックのDC成分に、以下のような改ざんがあったとします。

何個目のブロックか	前のブロックの値との差分	値
1	–	100
2	0	100
3	1	101
4	2	103
5	0	103

↓

何個目のブロックか	前のブロックの値との差分	値
1	–	100
2	0	100
3	-100(改ざんされている)	0
4	2	2
5	0	2

改ざんによって、改ざんされたブロック以降の値が根こそぎおかしくなってしまいます。

繰り返しますが、差分符号化が使われているのはDC成分だけで、AC成分は値そのものをイメージデータに記録します。

試しにイメージデータを見てみる

ある程度知識をインプットできたと思いますので、問題の画像の実際のイメージデータを見てみましょう。
1つめのブロックのY(輝度)の部分だけ取り出してみました。

何も分かりません…どういったルールで符号化されているかわからないためです。
符号化のルールについては DHTセグメントで定義されていますので、その内容を見ていくことにします。

DHTセグメントについて

概要

DHTセグメントは符号化するにあたって必要な情報が格納されています。
具体的にはどのような符号がどのようなデータと対応しているか、ということを定義しています。

また、DHTセグメントは普通、複数存在します。
問題の画像ファイルのDHTセグメントの部分だけ抜き出してきましたが、4つあります。

これは、下記の4つの成分ごとに違ったDHTが割り当てられているからです。

• 輝度(Y)のDC成分
• 輝度(Y)のAC成分
• 色差(Cb・Cr)のDC成分
• 色差(Cb・Cr)のAC成分

どのDHTセグメントがどの成分のものなのかは、DHTセグメントの後に続くSOSセグメントで定義されています。
詳細は省きますが、SOSセグメントの内容を読み解くと以下のような対応関係があることがわかります。

• 輝度(Y)のDC成分 → 1つめのDHTセグメント
• 輝度(Y)のAC成分 → 2つ目のDHTセグメント
• 色差(Cb・Cr)のDC成分 → 3つ目のDHTセグメント
• 色差(Cb・Cr)のAC成分 → 4つ目のDHTセグメント

輝度(Y)のDC成分を符号化/複号する時には
1つめのDHTセグメントに定義されたルールを参照する必要があるということです。
他の成分についても、それぞれに対応するDHTセグメントを参照して符号化/復号を行います。

DHTセグメントは何を表現しているのか

DHTセグメントは主にハフマン符号とその後に続くデータのビット数との関係を定義しています。
また、DC成分に対応するDHTセグメントと、AC成分に対応するDHTセグメントとでは内容が異なります。
まずは比較的単純なDC成分に対応するDHTセグメントの内容を見ていきます。

DC成分に紐づくDHTセグメント

実際に、輝度のDC成分に紐づくDHTセグメントの内容を見てみます。

詳細は省きますが、上記の内容は以下のような内容を示しています。

ハフマン符号	その後に続くデータのビット数
00	6
01	8
100	4
101	7
110	9
1110	5

例えばですが、 00101010..............というビット列があったとします。
先頭から読み進めていくと 00というビット列が存在することがわかります。
この 00というビット列は、上の表の一番上の行のハフマン符号を合致します。
表によれば、 00の後は6ビットのデータが続きます。
00の後の6ビットを切り出すと 101010です。
これはハフマン符号ではなく実データを示すので、10進数に変換すればデータ値が導けます。
101010 → 42
ということで、 00101010というビット列は、42というデータ値を示します。

以上のことから分かるように、ハフマン符号はデータ値そのものを示しているのではなく、データ長を示します。

ちなみに、「JPEGが圧縮されるまでの流れ」の項で示したように「DC成分→AC成分1つ目→AC成分2つ目…」という順番でデータが並んでいきます。
したがって、1つのDC成分の値を読み取ったら、その後に続く63個のAC成分を読み取る必要があります。

AC成分に紐づくDHTセグメント

今度はAC成分に紐づくDHTセグメントを見てみます。

詳細は省きますが、上記の内容は以下のような内容を示しています。

ハフマン符号	その前に0の成分がいくつ続くか	その後に続くデータのビット数
00	0	ブロックの終端まで0が続く(EOB)
010	0	1
011	0	2
1000	0	3
1001	0	4
1010	0	5
1011	1	2
11000	2	3
11001	3	3
11010	8	1
110110	1	1
110111	3	2
111000	5	1
111001	6	1
111010	7	1
1110110	1	3
1110111	1	4
1111000	2	2
1111001	2	4
1111010	3	4
1111011	9	1
1111100	12	1
11111010	4	1
11111011	11	1
11111100	13	1
11111101	15	0
11111110	15	1

DC成分のDHTセグメントと同じく、ハフマン符号がデータ長を示している、ということは変わりません。
ただ、以下の点が異なります。

1. ハフマン符号がデータ長だけではなく、その前に0の成分がいくつ続くかも示すようになっている
2. EOB(End Of Block)という概念が追加されている
   1. ZRL(Zero Run Length)という概念も追加されていますが、本記事では扱いません

以下のビット列をデコードしながら説明していきます。
01011100010100

先頭から読み進めると 010というハフマン符号が見つかります。(上の表の8行目)
このハフマン符号の後には1ビットのデータが続きます。そのデータは1です。
1という2進数を10進数に変換すると1(そのままです)になります。
したがって、AC成分の1つ目の成分の値は1ということがわかります。

AC成分はあと62個あるはずなので続けて読み取っていきます。
0101まで読み取ったので5ビット目から読み取ります。
すると、 11000というハフマン符号が見つかります。(上の表の8行目)
このハフマン符号の後には3ビットのデータが続きます。そのデータは 101です。
101という2進数を10進数に変換すると5になります。
したがって、2つ目のAC成分の値は5……..ではないです。
2つ目のAC成分ではなく、4つ目の成分の値が5です。
2つ目と3つ目のAC成分は？　0です。
なぜなら、ハフマン符号 101は、その前に値が0の成分が2つ続くからです(上の表の8行目を参照)。

残りのビット列を読み進めると 00というハフマン符号が見つかります。
これは上の表によると EOB(End Of Block)と紐づいています。
これは、ブロックの最後までずっと、値が0の成分が続くということを示します。
したがって、6つ目から63個目のAC成分は全て0になります。

総括すると、 01011100010100というビット列は
– 1つ目のAC成分 → 1
– 2つ目と3つ目のAC成分 → 0
– 4つ目のAC成分 → 5
– 5つ目~63個目のAC成分 → 0

という意味を持つことになります。

DHTセグメントの解析結果

4つのDHTセグメントの中身を解析すると、下記のような結果となります。
(一応載せてあるだけなので読み飛ばしてください)

輝度のDC成分を表現するときのハフマン符号(1つ目のDHTにて定義)

ハフマン符号	その後に続くデータのビット数
00	6
01	8
100	4
101	7
110	9
1110	5

輝度のAC成分を表現するときのハフマン符号(2つ目のDHTにて定義)

ハフマン符号	その前に0の成分がいくつ続くか	その後に続くデータのビット数
000	0	1
001	0	2
010	0	3
0110	0	4
0111	1	1
1000	1	3
1001	2	1
10100	0	ブロックの終端まで0が続く(EOB)
10101	0	5
10110	0	6
10111	1	2
11000	2	2
110010	0	7
110011	0	8
110100	3	1
110101	4	1
110110	4	2
110111	5	1
111000	6	1
111001	8	1
1110100	1	4
1110101	2	3
1110110	3	2
1110111	7	1
1111000	8	2
1111001	9	1
11110100	3	3
11110101	10	1
11110110	11	1
11110111	13	1
11111000	15	0
111110010	1	5
111110011	1	7
111110100	1	8
111110101	2	4
111110110	2	7
111110111	3	4
111111000	4	3
111111001	5	3
111111010	6	3
111111011	6	4
111111100	7	2
111111101	12	1
111111110	12	3

色差のDC成分を表現するときのハフマン符号(3つ目のDHTにて定義)

ハフマン符号	その後に続くデータのビット数
00	4
01	5
10	7
110	6
1110	3
11110	2
11110	8

色差のAC成分を表現するときのハフマン符号(4つ目のDHTにて定義)

ハフマン符号	その前に0の成分がいくつ続くか	その後に続くデータのビット数
00	0	ブロックの終端まで0が続く(EOB)
010	0	1
011	0	2
1000	0	3
1001	0	4
1010	0	5
1011	1	2
11000	2	3
11001	3	3
11010	8	1
110110	1	1
110111	3	2
111000	5	1
111001	6	1
111010	7	1
1110110	1	3
1110111	1	4
1111000	2	2
1111001	2	4
1111010	3	4
1111011	9	1
1111100	12	1
11111010	4	1
11111011	11	1
11111100	13	1
11111101	15	0
11111110	15	1

イメージデータを読み解く

問題の画像のイメージデータについて

では、今度こそイメージデータを読み取るための知識が揃ったのでやっていきます。

1ブロック目の部分のイメージデータを読み取ります。
この部分です↓

1ブロック目のイメージデータは以下の通りです。

DHTセグメントの内容と照らし合わせながら解析していくと、下記のことがわかります。
1つ目のブロックのY(輝度)

成分	ハフマン符号	その前に0の成分がいくつ続くか	成分の値(2進数)	成分の値(10進数)
DC	00	–	010100	-43
AC_1	010	0	001	-6
AC_2	000	0	1	1
AC_3	–	–	–	0
AC_4	1000	1	101	5
AC_5	10101	0	10100	20
AC_6	010	0	010	-5
AC_7	010	0	010	-5
AC_8 ~ AC_9	–	–	–	0
AC_10	11000	2	11	3
AC_11	010	0	010	-5
AC_12 ~ AC_13	–	–	–	0
AC_14	1110101	1	101	5
AC_15	001	0	01	-2
AC_16 ~ AC_23	–	–	–	0
AC_24	1111000	8	01	-2
AC_25 ~ AC_39	–	–	–	0
AC_40	11111000	15	–	0
AC_41 ~ AC_47	–	–	–	0
AC_48	1110111	7	0	-1
AC_49	000	0	1	1
AC_50	000	0	0	-1
AC_51	000	0	0	-1
AC_52	110010	0	1110101	117
AC_53	000	0	0	-1
AC_54	–	–	–	0
AC_55	1000	1	111	7
AC_56	10100	0	–	0(EOB)
AC_57 ~ AC_63	–	–	–	0

続いて色差(Cr・Cb)もまとめて読み取ります。

1つ目のブロックのCr(色差)

成分	ハフマン符号	その前に0の成分がいくつ続くか	成分の値(2進数)	成分の値(10進数)
DC	00	–	0001	-14
AC_1	00	–	–	0(EOB)
AC_2 ~ AC_63	–	–	–	0

1つ目のブロックのCb(色差)

成分	ハフマン符号	その前に0の成分がいくつ続くか	成分の値(2進数)	成分の値(10進数)
DC	01	–	11001	25
AC_1 ~ AC_8	–	–	–	0
AC_9	11010	8	0	-1
AC_10	011	0	00	3
AC_11	1000	0	110	6
AC_12	1010	0	01110	-17
AC_13	00	0	–	0(EOB)
AC_14 ~ AC_63	–	–	–	0

改ざん前のイメージデータについて

急ですが、もう一度イメージデータのビット列を見てください。

↑のビット列は、 {}で囲った部分を意図的に改ざんして作りました。
改ざん前のイメージデータはこんな感じでした。

ちなみに、改ざん前のイメージデータはこのように綺麗な画像になります。

ということは、画像がおかしくなった原因として、改ざんした部分が関わっていそうだということが分かります。
なぜ画像がおかしくなったかを調べるためにも、改ざん前の画像についても同じように解析していきます。
そうすると、改ざん後の画像とは解釈が異なっていることがわかります。

1つ目のブロックのY(輝度)

成分	ハフマン符号	その前に0の成分がいくつ続くか	成分の値(2進数)	成分の値(10進数)
~ AC_49	変更前の画像と同じ	同じ	同じ	同じ
AC_50	10100	0	–	0(EOB)
AC_51 ~ AC_63	–	–	–	0

AC_50(50個目のAC成分)について注目してください。
改ざん後の画像では0という値でしたが、改ざん前の画像では EOB(ブロックの最後まで0)に変わっています。
こうなっているせいで、酷いことが起きています。

改ざん後の画像では AC_50は普通の値なので、次は AC_51、 AC_52…と続いていきます。
一方で、改ざん前の画像では AC_50が EOBなので、次に続くビット列はCr(色差)のものになります。
したがって、ビット列のうち一部しか変わっていないのに、それ以降のビット列の解釈に差が生まれていました。

こういったイメージです↓

実際にそれ以降に続くCr(色差)、Cb(色差)の値も、修正前のものに比べると大きく変化していることがわかります。

1つ目のブロックのCr(色差)

成分	ハフマン符号	その前に0の成分がいくつ続くか	成分の値(2進数)	成分の値(10進数)
DC	111110	–	1011101	-162
AC_1	010	–	0	-1
AC_2	00	–	–	0(EOB)
AC_3 ~ AC_63	–	–	–	0

1つ目のブロックのCb(色差)

成分	ハフマン符号	その前に0の成分がいくつ続くか	成分の値(2進数)	成分の値(10進数)
DC	10	–	0011110	-97
AC_1	1000	0	000	-7
AC_2	010	0	0	-1
AC_3	011	0	10	2
AC_4	011	0	10	2
AC_5	1000	0	110	6
AC_6	010	0	0	-1
AC_7	011	0	01	-2
AC_8	010	0	0	-1
AC_9 ~ AC_13	–	–	–	0
AC_14	111000	5	1	1
AC_15	010	0	0	-1
AC_16	00	0	0	0(EOB)
AC_17 ~ AC_63	–	–	–	0

なぜ画像がおかしくなっていたのか？

以上の観察から、なぜ画像がおかしくなっていたのかを考察します。

改めて、問題の画像を載せておきます。

この画像には以下のような特徴がありました。

1. 左上の市松模様のようなノイズが何個か続いている
2. 元画像と比べて、全体的な色味が赤っぽくなっている

左上の市松模様のようなノイズが何個か続いているのはなぜか？

1つ目のブロックの輝度に対応するイメージデータの一部が、本来あるべきものと異なっていたためです。
これにより、1つ目のブロックの色差、および2つ目以降のブロックの解釈の仕方も連鎖的におかしくなっています。

どこかのタイミングで帳尻が合ったために、途中からノイズがなくなったと推測できます。
(ノイズがなくなった以降のブロックは正常にデータを解釈できていると推測できる)

元画像と比べて全体的な色味が赤くなっているのはなぜか？

これも、1つ目のブロックの輝度に対応するイメージデータの一部が、本来あるべきものと異なっていたためです。
また、ノイズがなくなった後も赤くなっているのは、DC成分の符号化方法である「差分符号化」のためです。

「⑤エントロピー符号化」の項でこのように説明していました。

この差分値だけで表現する方法を差分符号化と呼びます。
差分符号化は、表現したいデータの値が似通っている時にはデータ量を少なくできる(圧縮できる)という利点があります。
一方で、データの改ざんにはめっぽう弱いという弱点があります。

1つめのブロックでデータの変化が起きていたのが原因で、それ以降のDC成分の値もおかしくなってしまいました。
ノイズが消えた後のブロックについては、正常にデータを解釈できていると思われますが、
それ以前のDC成分の値がおかしかったために、その影響を受けてしまっています。
差分符号化の「データの改ざんにはめっぽう弱い」という弱点を突かれた形になります。

また、DC成分は全体的な色味を左右します。
こういうこともあり、全体的な色味が赤くなってしまっていました。

最後に

最後まで読んでいただき、ありがとうございます。
レコチョクでは、ソフトウェア開発だけでない幅広い技術を経験する環境でチャレンジしたいメンバーを募集しています。
レコチョクに興味をお持ちの方は、レコチョクの採用ページをぜひご覧ください。

明日の レコチョク Advent Calendar 2023 は20日目 Android Graphics Shading Languageって何？ です。お楽しみに！