2023-11-21JPEG, 圧縮処理, 画像処理

レコチョクでバックエンドエンジニアをしている小河です。
レコチョクが運営するサービスが提供する、画像や音源などをメディアファイルを配信するシステムを担当しています。

前段

巷にありふれている画像圧縮方式の一つにJPEGが存在します。
本当によく見かける圧縮方式ですが、実はJPEG画像を生成する際に「品質」を設定することができます。

例えばこういった画像があるとします。

この画像はPNG形式なので、JPEG形式に変換したいとします。
ImageMagickを使えば容易に行えます。
この時、 -qualityオプションを指定することで「品質」もついでに指定できます。
100を最大として、このように指定します。

こうして出来上がった画像がこちらです。
綺麗な感じですね。

では、ちょっと極端ですが、 -qualityに10を設定してみます。

ガビガビになりました。見るに堪えない感じです。

ところで、品質( -quality)を設定すると、JPEG画像の何が変わっているのでしょうか？
-quality 10の画像はなぜあんなにガビガビになってしまうのでしょうか？
今回の記事ではその疑問を解消していきます。

目次

• 品質の違うJPEG画像を比較する
• 信号を周波数成分に分解する
• 画像を周波数成分に分解する
• パワースペクトルをいじってみる
• JPEGの圧縮の全体像
• DCTとは
• 量子化とは
• DQTとは
• なぜ10.jpgは粗くて100.jpgは綺麗なのか
• 品質とデータ容量の関係
• まとめ
• ちなみに
• 参考

品質の違うJPEG画像を比較する

ひとまず、品質の高くて綺麗な 100.jpgと品質が低くてガビガビな 10.jpgをバイナリベースで比較してみます。
いきなり16進ダンプの結果を比較しても辛いだけなので、fqを使って楽をします。
fqに画像ファイル(動画でもなんでも良いですが)を読み込ませてあげると、どのようなセグメントにどのような情報が入っているかを分かりやすく表示してくれます。

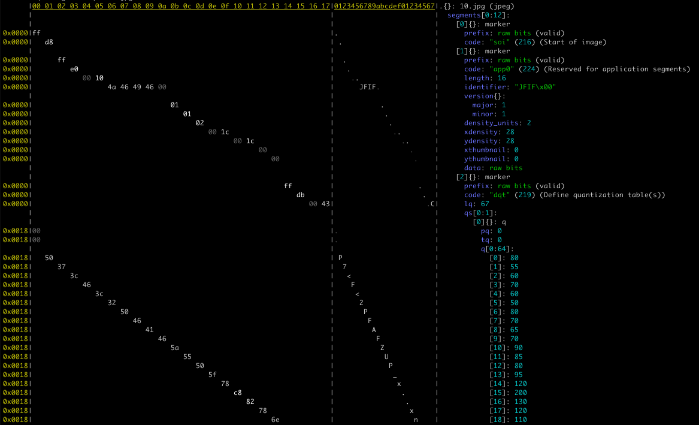
では、 10.jpgと 100.jpgをそれぞれfqにかけた結果についてdiffを取ってみます。
そうすると、画像で示した部分の差分が特に目立ちます。

※ 赤いところが差分があった部分、紫色のところは差分がなかった部分を示します。
※ 左が 10.jpg、右が 100.jpgを示します。

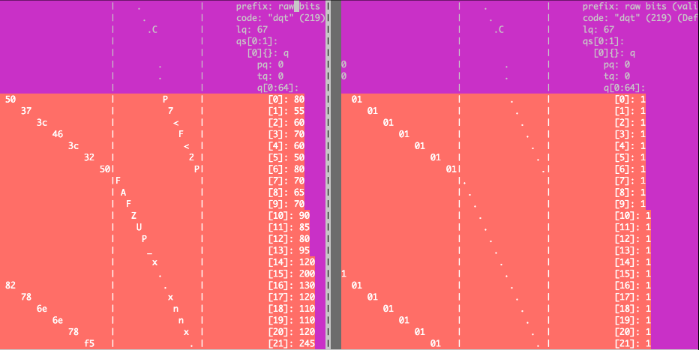
左の 10.jpgは100を超えるような大きい数値ばかりが含まれており、右の 100.jpgについては1ばかりです。
切れて見えていませんが 10.jpgの方は255のような値も現れたりする一方、 100.jpgはずっと1です。

はい、こここそが品質の良し悪しに非常に大きく関係しているDQT(Define Quantization Table:量子化テーブル)と呼ばれる部分です(わざとらしくてすみませんが)。
設定する品質が違えばこのDQTの値も異なってきます。
したがってここが親玉です。

では、DQTは一体何を表すのかを説明したいのですが、、、前提知識が必要となります。
少し長くなりますが、「信号を周波数成分に分解する」ことや「JPEGの圧縮方法の概要」についてまず話をさせてください。
また、以降については簡単のために厳密さを欠いた説明となっていますので、どうかご容赦ください。

信号を周波数成分に分解する

全ての信号は正弦波という非常な単純な波の組み合わせで表現することができます。
実際に見てみましょう。
上半分の信号を、単純な波に分解した図が下半分のグラフです。
下半分のグラフはパワースペクトルと呼ばれ、どの周波数の波がどのくらい含まれているかを示します。
横軸は周波数(どれだけ細かい波か)、縦軸は振幅(波の大きさ)を示します。

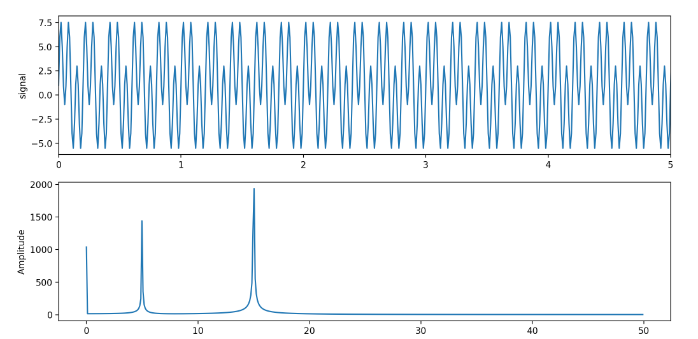
したがって、複雑そうな信号が、0Hzの波、5Hzの波、15Hzの波に分解されたことが表されています。
単に周波数成分に分解されたということもできます。
周波数成分というのは0Hzの波、5Hzの波のような、xHzの波の総称です。

0Hzの波というのは常に一定の値を示す成分のことです。
この0Hzの波のことを直流成分(DC成分)と呼びます。
反対に5Hzの波のように、値の変化がある成分のことを交流成分(AC成分)と呼びます。

ところで、信号のことと画像の間に何の関係があるのか、という話です。
音声や画像も所詮は数値の羅列ですので、これらも信号と捉えることができます。
したがって、画像も先ほどやったように周波数成分へ分解することが可能です。

画像を周波数成分に分解する

では、画像も実際に周波数成分へ分解してみます。

こうなりました。

一番左が分解前の元画像、真ん中が周波数成分を表したもの(パワースペクトル)、一番右がパワースペクトルから画像を復元したものとなります。
一つ前の項で説明した信号のパワースペクトルは2次元のグラフでしたが、今回のパワースペクトルは3次元(縦・横・色の濃さ)です。
これは元とする信号が画像という2次元のデータであるためです。

パワースペクトルの見方を説明します。
まず、色についてですが、白に近ければ近いほど多くの成分を含んでおり、反対に黒に近いほど少ない成分しか含まれていないことを示します。

縦は、縦方向の周波数を表します。つまり、どのくらいの横縞模様のような成分がどれだけ含まれているかを示します。
下に行けば行くほど高い周波数成分を示します。なので、下に行けば行くほど細かい横縞模様のような成分を示します。

横は、横方向の周波数を表します。つまり、どのくらいの縦縞模様のような成分がどれだけ含まれているかを示します。
右に行けば行くほど高い周波数成分を示します。なので、右に行けば行くほど細かい縦縞模様のような成分を示します。

ちなみに、斜め右下に行けば行くほど、細かい市松模様のような成分がどれだけ含まれているかを示します。(横縞と縦縞を合成すると市松模様のようになるので)
また、一番左上の部分は波のない直流成分を示します。それ以外は交流成分となります。
直流成分は画像全体の色味を表し、交流成分は色の変化を表すことになります。

ちょっと受け入れ難いですが、このように画像も単なる波の組み合わせで表現できてしまいます。

パワースペクトルをいじってみる

前項でもやっていましたが、パワースペクトルから元の画像を復元することができます。
ところで、パワースペクトルをいじってから画像の復元をしてしまったらどうなるのでしょうか？
やってみましょう。

高い周波数成分を削ってみます。
パワースペクトルにおいて、右や下に行くほど高い周波数成分を示すのでした。
では、パワースペクトルの右下あたりをごそっと削ってしまいます。
それを復元するとこうなります。
※ 中央のパワースペクトルの影になっている部分は、成分を削っている部分を指します

ちょっとぼやけましたね。
高い周波数成分は細かい色の変化を司っています。
それを削った結果、このような細かい模様の表現に難が出てきた、ということです。

ちなみにもっと削ってみると、もっとぼやけます。

では、反対に低い周波数の部分を削ってしまうことにします。
先ほどとは反対に、パワースペクトルの左上の部分を削ってしまいます。

原型がなくなってしまいました。
なんとなく、輪郭が写っている気がしますが…

削る部分を少なくしてみます。

元の画像には近づきましたが、依然としてめちゃくちゃなままです。
被写体の輪郭は残っていますが、全体的な色味など、大切なものが根こそぎ失われたままです。

以上の実験からこのようなことが読み取れます。

• 高い周波数成分を削ってしまっても、(比較的)画像の見た目に影響を与えない
• 低い周波数成分を削ってしまうと、画像の見た目に甚大な影響を及ぼす

したがって、画像をうまく圧縮したいと思ったら、高い周波数成分から削った方が良いということになります。
画像の見た目の影響を抑えつつ圧縮できるからです。
JPEGでもこの手法が使われています。これについては後の「量子化」の項で取り上げます。

JPEGの圧縮の全体像

JPEG形式へ画像が圧縮されるまで、以下のような処理が施されます。
(JPEG画像を画像として表示する際は、これとは逆順に処理が施されることになります)

JPEGでは、画像全体に対してそのまま処理を施すのではなく、8×8(64ピクセル)ずつに分けて行います。
なので、8×8の小さな画像に対してエントロピー符号化まで行われて、最後に結果が全て結合されます。

あとは、それぞれの処理内容について説明します。
最後の「エントロピー符号化」は今回扱いたい内容からは外れるため、DCTと量子化の説明をします。

DCTとは

DCT(離散コサイン変換)とは信号を周波数成分に分解する手法の一つです。
周波数成分へ分解する手法として一番有名なのがフーリエ変換ですが、JPEGではDCTが用いられています。

実のところ、DCTは今回の記事の中で既に登場しています。
「画像を周波数成分に分解する」という項で画像からパワースペクトルの変換を行なっていました。
この変換にDCTを用いていました。
JPEGへの圧縮では、画像全体に対してではなく8×8の小さな画像に対してDCTが行われます。
このDCTの後に出力されるパワースペクトル上の値一つ一つをDCT係数と呼びます。

量子化とは

量子化というのは連続値を離散値へ変換するプロセスのことです(一般に言われる「量子化」と同じ)。
今回はDCTを行なった後に出力されるDCT係数を低い精度となるよう量子化します。

また、純粋に量子化するだけではなく、周波数成分(DCT係数)ごとに重みをつけて量子化します。
具体的には、高い周波数成分のDCT係数については粗く量子化し、低い周波数成分については比較的細かく量子化します。
なぜなら高い周波数成分を削った方が画像の見た目に影響を及ぼしにくいからです(「パワースペクトルをいじってみる」の項でも明らかになったことです)。

以下のように量子化されます。

式について説明します。
「量子化されたDCT係数」は低い精度へ丸められてしまうので、その分の情報は捨てられます。
JPEGを画像として表示する際、量子化されたDCT係数を元に戻すわけですが、
その際、失われた情報分、表示される画像は元画像から離れたものとなってしまいます。
(これがJPEGが非可逆圧縮形式にカテゴライズされる所以の一つです)

量子化ステップは定数を取ります。
したがって、DCT係数がどの周波数成分のものであっても同じ値を取ります。
ただ、これではDCT係数ごとに重みをつけて量子化できません。
そこで量子化テーブル数です。この値はDCT係数ごとに違った値を取ります。
量子化テーブル数は1から255までの値を取り、255に近づくほど粗い粒度で量子化されます。

この量子化テーブル数はJPEGファイル内のDQTに記録されています。

DQTについては「品質の違うJPEG画像を比較する」という項で「品質のパラメータを変化するとDQTの値も変化する」ということを説明したっきりでした。
次の項で説明していきます。

DQTとは

DQT(Define Quantization Table:量子化テーブル)とは、「画像に含まれるどのような周波数成分ごとに、どういった粒度の量子化を行うかを定義した8×8のテーブル」です。
JPEGファイルの中では 80 55 60 70 60 50 80 70...(本当は2進数で表します)というように数値の羅列でDQTは表現されていました。
本来は「テーブル」という名を持つこともあり、このような構造を持ちます。

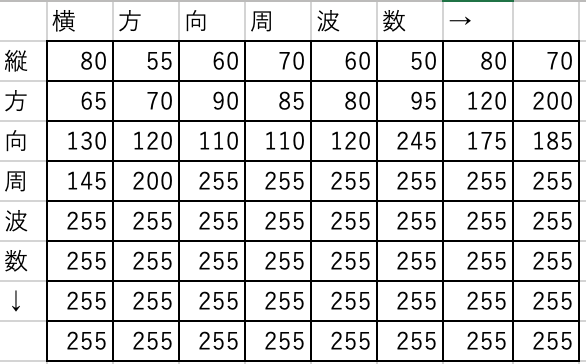
これは、周波数成分ごとにの量子化テーブル数を示しています。
パワースペクトルと同じく、下に行けば行くほど高い縦方向の周波数について示します。
反対に、右に行けば行くほど高い横方向の周波数について示します。
数値に関しては、先ほども説明した量子化テーブル数の値そのままです。

今回取り上げたDQTは高周波数の成分について255という最大の量子化テーブル数が設定されています。
したがって、高周波の成分(画像の細かい部分)は粗く量子化された(＝より多くの情報が失われた)ということです。
そのようなJPEG画像を表示させると、失われた情報分、画像が荒く見えてしまいます。

なぜ10.jpgは粗くて100.jpgは綺麗なのか

ようやく最初の話に戻ります。
この記事はそもそもこのような主旨でした。

ところで、品質( -quality)を設定すると、JPEG画像の何が変わっているのでしょうか？
-quality 10の画像はなぜあんなにガビガビになってしまうのでしょうか？
今回の記事ではその疑問を解消していきます。

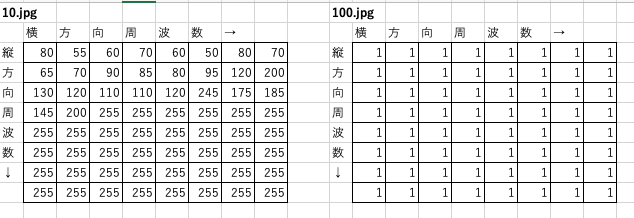
結論 10.jpg(品質を低く設定したもの)はDQTの値が比較的大きく、 100.jpg(品質を高く設定したもの)はDQTの値が比較的小さいからです。

10.jpgと 100.jpgのDQTを比較してみると、実際にそのようになっていることがわかります。

品質とデータ容量の関係

品質が低いことは悪いことばかりかというと全くそうではなく、データ容量については優位です。
品質の高い 100.jpgの容量は291KBである一方、品質の低い 10.jpgは8KBです。
あくまで目的に合わせて品質を調節する必要があります。

ImageMagickの場合ですが、品質( -quality)を85に設定するとバランスが良いという話もありますので、
特に意味がなければ85に設定するのが良いかと思います。

画質が 85 を超えている場合は、85 に下げます。画質が 85 を超えると画像の容量が急増しますが、視覚的な品質はほとんど向上しません。
https://developers.google.com/speed/docs/insights/OptimizeImages?hl=ja

まとめ

• JPEG画像への変換の際は「品質」を設定できる
• 「品質」はDQTの値に影響する。具体的には「品質」が低いほど、DQTの値も大きくなる
• DQTは周波数成分ごとに、どれくらいの粒度で量子化を行うかのパラメータ
• DQTは見た目に大きな影響の出ない高周波成分を優先して、荒く量子化するようにパラメータが設定される
• 「品質」を操作する → DQTの値が変わる → 量子化の粒度が変わる → JPEG画像の見た目に影響が出る
• 「品質」が高いほどデータ容量は大きくなる

ちなみに

品質に関わる要素としてDQTだけではなく、サンプリング比も存在します。
サンプリング比は画像のRGB値をYCbCr値(輝度・色差)に分解し、その輝度と色差についてどのような割合で情報を間引くかという情報を示します。
正直よくわからないと思いますが、数値が小さい方が多く情報が間引かれている(品質が低くなる)と理解ください。

サンプリング比はexiftoolによって確認できます。
10.jpgと 100.jpgで比較してみると、サンプリング比が違うことがわかります。

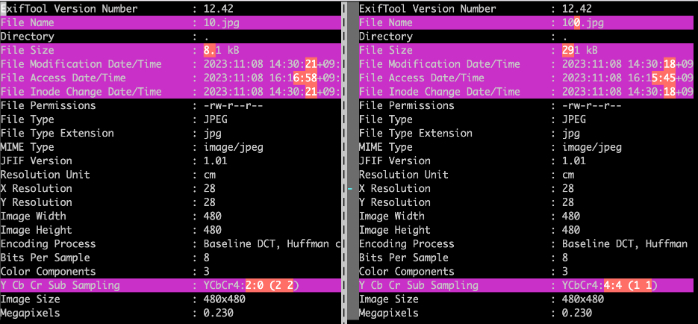
10.jpgは 4:2:0で 100.jpgは 4:4:4ですから、 10.jpgの方がサンプリング比によって情報が多く間引かれていることが分かります。
これが結果的に品質の低下につながります。

参考

そこが知りたい最新技術 オーディオビデオ圧縮入門(インプレスRD)
詳解 圧縮処理プログラミング (SBクリエイティブ)
JpegAnalyzer Plusオンラインヘルプ

最後に

最後まで読んでいただき、ありがとうございます。
レコチョクでは、ソフトウェア開発だけでない幅広い技術を経験する環境でチャレンジしたいメンバーを募集しています。
興味のある方は、レコチョク (採用ページ)からぜひご応募下さい。